The most frequent line call in doubles tennis is that of whether a serve is in or out on the back line of the service area.  The call can be contentious.   Convivial tennis means giving the “benefit of the doubt” and only calling a ball out when it is clearly so¹.   Since a ball is in if its impact includes any part of the line, this means one should “see paint” – some portion of the court between the line and the ball – before calling a ball out.

The rule in doubles tennis is that if either of the receiving partners thinks the ball was in, then the call is that the ball is in².

The rules are clear and the rules should be followed in any tennis match; they are meant not just for accuracy but also to make the game civilized and enjoyable.

But here I want to narrow purely to accuracy.   I want to ask the following:

If three players – the server, the receiver, and the receiver’s partner (the partner), in typical doubles formation – all make a call on whether a ball is in our out, who is most accurate and by how much?

The surprising result is that geometry advantages the partner so that his or her call is more accurate by a factor of 6 than the receiver and by a factor of 60 than the server.   For intuition, though the partner is a little closer to the impact than the others, a much bigger effect comes from the fact the other observers are trying to discriminate a small displacement nearly parallel to their boresights, but the partner is trying to discriminate one nearly orthogonal to his. In the limit, a displacement completely orthogonal to boresight produces maximal displacement on the retina (best case for accuracy), while one completely parallel to boresight produces no displacement on the retina (worst case for accuracy).    The discrepancies in accuracy are so large that it would be best to defer to the receiver’s partner over either the receiver or the server or the combination of both.  

As a graphical aid, imagine you have three people giving you their opinions about whether two close together lines on a wall are separate or not, and they are arranged spatially as shown.   How would you weigh their opinions? Would you be surprised if the two to the right couldn’t see the lines as separate while the one on the left could? (The spacing here is to scale.) To put it another way, if one observer has uncorrected 20/20 vision and another has uncorrected 20/120 vision, would it surprise you that the first one can see details that look blurred to the second? Let alone 20/1200 vision.

The Physiology of Calling a Serve

An observer calls a ball out by “seeing paint” – observing a segment of court between the line and the ball.  Observers are limited by their visual acuity.  Visual acuity is determined by the physiology of vision: the combination of the eye’s optics, possibly corrected by glasses or contacts, and the spacing of the cells on the retina, specifically the cones in the fovea.  

If the spacing of two lines is close enough on the retina, then there will not be sufficient space for independent cones to detect the separation between the lines and they will appear blurred together.

So, assuming the same (possibly corrected) vision for two observers ³, the key question is how far about are same two lines on the retina as seen from each observer’s position: how much better can one observer resolve the lines than another?

The Geometry of Calling a Serve

We place the three players in space in a typical formation.

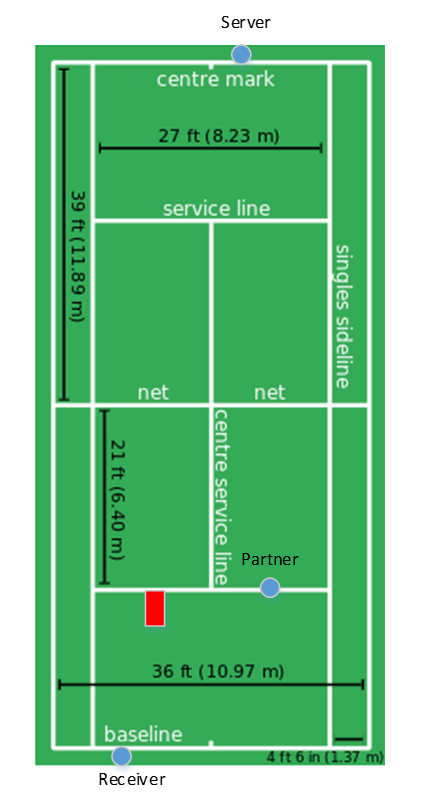
All three players are trying to determine the length of the long side of the red block (how far a serve is long).  Their ability to resolve the length is determined by the angular resolution it subtends on the retina.   The smaller the angle, the less likely they can resolve it.

We can pick some small, arbitrary length for the red block, then figure the angles subtended on the retinas of each of the observers and compare them.   I use the length 1” = 0.0254m in the calculations below.

We can determine those angles exactly by computing the lengths of the side of the triangle formed by each observer and the two ends of the block, then applying the law of cosines.

We assume that each observers’ eye is 5’ 8” (1.727 m) above the court and that the observers and block are the following locations.

• The server is at a point 2.000 m from the center mark on the serving baseline.
• The receiver is at point 3.000 m from the centre mark on the receiving baseline.
• The red block has its endpoints on the line between the feet of the server and receiver (i.e., on the surface of the court) with one end on the service line.  (Note that this is slightly different than the diagram; the block is not perpendicular⁴ to the service line and the difference from perpendicularity does reduce the angle subtended on the retina of the partner.  The math captures this effect exactly.)
• The partner is 1m from the centre service line and on the service line.

We can then compute the 3-D coordinates for each point, using the origin as the lower left of the diagram and on the court; the x direction is along the baseline, the y direction is along the sideline, and the z direction is height above court.

Point	x	y	z
Server	7.486	23.774	1.727
Receiver	2.486	0.000	1.727
Partner	6.486	5.486	1.727
Service Line end of Red Block	3.640	5.486	0.000
Other end of Red Block	3.635	5.462	0.000

 We can compute the lengths of the sides of each triangle and then apply the law of cosines  – where a and b are the two sides from the observer to either end of the block and c is the length of the block:

The result is

Observer	Angle in Degrees Subtended on the Retina of the Observer	Factor by which the Partner is more Accurate than the Observer
Server	0.0071	60
Receiver	0.0733	6
Partner	0.4297	1

Interpretation

The geometry is stark. It doesn’t make sense to defer to either the Receiver or a joint conclusion of the Receiver and the Server for this specific call; they are simply too relatively inaccurate to stand alone or to reap a useful advantage from combining the two (the server is so inaccurate relative to the receiver that there is no advantage to combining with the receiver’s).  In simple terms, the receiver and server are so much less accurate in making this particular call that they should simply be ignored. Of course, by the rules, the receiver would not be ignored (though the server would); notwithstanding much lower accuracy, if he or she calls the ball in when the partner has called it out, it is in. This both follows the rules while being (usually) less accurate.

My personal recommendation how to reflect both relative accuracy and the rules is the following:

• If I am the receiver, I wait for my partner to make an out call for serves near the service line (I assume no call will be stated if he or she thinks the ball is in). If he or she makes an out call on the service line and I am sure the ball was in (I am convinced I saw paint the other way) then I will dispute the call. But I need to be sure – saying that I wasn’t sure and that the ball may have been “on the line” (and so should give the server the benefit of the doubt) doesn’t imply that my partner was not or could not have been sure of an out call. Note that calling serves that are wide rather than long is different and it is quite possible that I have better geometry than my partner in making such calls – for the same reason of parallel versus orthogonal to boresight.
• If I am the partner, I try to make a call immediately for balls that are long and only if I can “see paint” between the ball and the service line. Other than needing to see paint, I don’t try to bias my calls either way.
• If I am the server or server’s partner, I do not comment on the receiving side’s call as to whether my serve was in or out but simply accept it at face value. I do not try to contribute to or weigh in on any dispute between the two of them. If they disagree, the ball is in.

And What About Hard, Flat Serves

It gets more difficult to judge where the ball landed as a serve increases in velocity and flattens for two reasons:

1. The time of the event shortens, and the human visual system’s ability to perceive events degrades with reduced time.
2. The time and location of the bounce is detected by an observer from a reversal in the vertical component of velocity, and as the serve flattens the size of that component shrinks making it harder to detect its reversal.

These effects are felt by all observers.

Because the Receiver and Server are so much less accurate than the Partner, as the serve gets harder and flatter, resolving a long call will drop below their ability to resolve well before it does for the Partner.  They will judge a call as “too close to call” before it would be necessary or appropriate for the Partner to also conclude that – since he or she is still in a position to resolve the displacement.  

Few slower serves will be close enough to the service line to engender a disagreement in whether one could “see paint” or not between the receiver and partner, but a significantly larger fraction of hard, fast serves will.

For Future Work

Several people have critiqued, commented on, and asked questions about this analysis. I try to capture those here for further investigation.

Source	Observation/Question	Initial Thoughts
Rick Shaughnessy	Schrodinger’s work suggests the serve can both be in and out at the same time.	Deep. Will take some time to fully address. What is the quantum wave function of a tennis ball?
Keith James	What if the ball is spinning and its trajectory is curved?	Can probably model this by changing the orientation of the line segment to be something other than in the line from server to receiver. But spinning serves are often slower than hard flat serves (at least in our very non-professional group), so the issue doesn’t come up as much (meaning for slower serves the cases where observers differ are more rare).
Keith James	The receiver observes the flight of the ball from a different angle than the partner and the partner observes it for a shorter period of time.	I’m not following this yet, will consult with Keith. To my mind they both observe the ball for the same period of time (at least I do when playing each of these positions) and both attempt to keep the ball in the center of their field of vision with similar success. The key is the distance to and relative angle of the line segment (“the paint”) they are trying to judge at impact.
Michel Schmied	The partner may tilt his head.	I’m not sure how general it is that people tilt their heads when observing the serve, but I am assuming that the fovea is rotationally symmetric which would make that irrelevant. Worth checking how true that is.
Michel Schmied	What about the server’s partner and their potential contribution to the decision?	At first, I dismissed this as the math shows the server is so far away as to be essentially irrelevant – if the partner was lined up on the baseline too as sometimes happens, they would be too. But I now think Michel has a point – the server’s partner is much closer than the server in typical formation, as Michel says, and is not as close to sighting along boresight, so has a better angle. From the rules, the server’s partner has nothing to say about whether the serve is in or out, but from an optimal decision perspective they might. Do have to be sure their vision isn’t obscured by the net, though.
Tom Lookabaugh	What is the optimal way to combine binary decisions of different accuracy to make an overall binary decision? Beyond simply using the most accurate when accuracies vary widely, or some kind of vote when decisions are of similar accuracy, is there an optimal algorithm?	It seems to me that all possible binary functions of a set of binary inputs are determined by a truth table. For a small number of inputs, there simply aren’t that many possible truth tables (for n inputs, there are 2n possibilities). So, if we knew the probability of error for each input, and assumed the errors are independent, we could simply check the output error probability for each possible truth table and pick the one with the lowest error. This ought to generate both the “only use the best one” and “vote” outcomes for different distributions of error probabilities on the inputs and possibly other functions (though I’m not sure what they are). Things might get a little more interesting if we allowed a “not sure” possibility and made the inputs ternary. For further work…
Keith James	What if the partner crouches down so that his or her eyeball is much lower, in the range of 4′ to 4′ 6″?	This of course depends on stature; Rick, for example, is likely still above 5′ when crouched. But running the numbers when both the receiver and partner crouch by the same amount actually increases the relevant discrepancy in accuracy (the receiver is even more impacted by trying to discriminate distance along boresight while the partner sees little effect in trying to discriminate distance orthogonal to boresight). Still, what if only the partner crouches? Should be easy to calculate though my expectation is that it has little effect for the “still pretty much the same orthogonal to boresight” reason.
Michel Schmied	The partner may be lined up ahead of the service line rather than on it.	When I play the partner position, I line up on the service line to judge the serve, then step forward after that to play the rest of the point. It is true that if the partner lines up in the middle of the box, he or she will lose some of the advantage of orthogonality to boresight and that effect is calculable.

---

1. “Opponent gets benefit of doubt. When a match is played without officials, the players are responsible for making decisions, particularly for line calls. There is a subtle difference between player decisions and those of an on-court official. An official impartially resolves a problem involving a call, whereas a player is guided by the unwritten law that any doubt must be resolved in favor of the opponent. A player in attempting to be scrupulously honest on line calls frequently will find himself keeping a ball in play that might have been out or that the player discovers too late was out. Even so, the game is much better played this way.” Section 6 of The Code – The Player’s Guide for Matches When Officials are Not Present ↩︎
2. “Partners’ disagreement on calls. If one partner calls the ball out and the other partner sees the ball good, they shall call it good.”  Section 14 of The Code – The Player’s Guide for Matches When Officials are Not Present. ↩︎
3. My own uncorrected distance vision is 20/15.  My distance vision has been improving at the cost of my near vision which now requires significant correction with reading glasses ↩︎
4. It is 11.9 degrees off of perpendicular based on the specified server and receiver positions assuming the ball travels from server to receiver. ↩︎